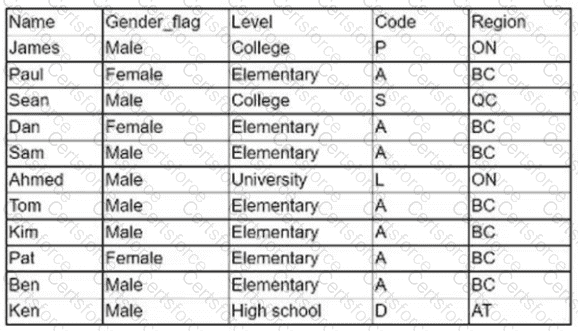
The logical statement that results in Table B is Option D. Option D is a logical statement that uses the AND operator to combine two conditions: Name = “Tom” and Region = “BC”. The AND operator returns true only if both conditions are true, otherwise it returns false. Therefore, Option D will select only the rows from Table A that satisfy both conditions, which are rows 4, 5, 6, and 7. These rows form Table B, as shown below:
Name | Gender flag | Level | College | Code | Region Tom | Male | Elementary | A | BC | BC Kim | Female | Elementary | A | BC | BC Pat | Female | Elementary | A | BC | BC Ben | Male | Elementary | A | BC | BC
The other options are not correct, as they use different logical operators or conditions that do not result in Table B. Option A uses the OR operator, which returns true if either condition is true, or both. Option A will select all the rows from Table A except row 3, which does not match either condition. Option B uses the NOT operator, which returns the opposite of the condition. Option B will select all the rows from Table A except rows 4, 5, 6, and 7, which match the condition. Option C uses a different condition, Region = “ON”, which does not match any row in Table A. Option C will select no rows from Table A. Reference: [SQL Logical Operators - W3Schools]
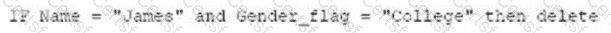
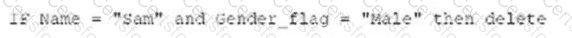
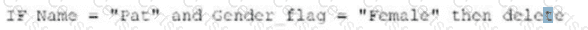
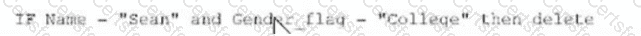
Submit