To see how this is done, let W represent the event that the conversation was held with a woman, and L denote the event that the conversation was held with a long­haired person. It can be assumed that women constitute half the population for this example. So, not knowing anything else, the probability that W occurs is P(W) = 0.5. Suppose it is also known that 75% of women have long hair which we denote as P(L |W) = 0.75 (read: the probability of event L given event W is 0.75, meaning that the probability of a person having long hair (event "L"): given that we already know that the person is a woman ("event W") is 75%). Likewise, suppose it is known that 15% of men have long hair, or P(L |M) = 0.15; where M is the complementary event of W: i.e.; the event that the conversation was held with a man (assuming that every human is either a man or a woman).

Our goal is to calculate the probability that the conversation was held with a woman, given the fact that the person had long hair, or, in our notation, P(W |L). Using the formula for Bayes' theorem, we have:

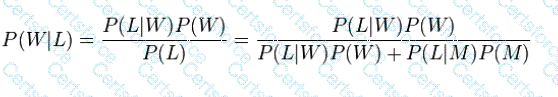Text Description automatically generated with low confidence

where we have used the law of total probability to expand

P(L),

The numeric answer can be obtained by substituting the above values into this formula (the algebraic multiplication is annotated using " *", the centered dot). This yields

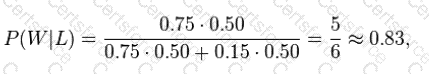A picture containing table Description automatically generated

i.e., the probability that the conversation was held with a woman, given that the person had long hair is about 83%. More examples are provided below.